Shot quality is a polarizing issue within the hockey stats community. Its relevance and value has been examined in various ways by many people and debated endlessly. To avoid a history lesson, I’ll keep the introduction to this topic brief, but I recommend conducting some additional research to anybody interested in learning more. It’s foremost important to understand nobody (worth listening to) has or will argue that shot quality does not exist. That some shots are better1Let’s get this out of the way early. “Better” in this article will refer to a greater probability of becoming a goal. than others is a core tenet of hockey and indeed any such sport. Questions like “What makes a shot better?” or “Can players have a sustainable influence on shot quality?” are much more interesting questions. As is often the case with such things, answering these questions can prove tricky.
It is by virtue of work done by Eric Tulsky and others that we’ve come to question the importance of shot quality in our analysis, and it is by virtue of our intuition that we continue to pursue a better shot quality formula despite this.
The crux of people’s skepticism towards the relevance of shot quality in hockey analysis is the variance in this measure that has been observed at both the team and player levels. Hockey is fraught with randomness and this imposes limitations on one’s ability to predict future outcomes or performance.2People have used this fact to disparage the usefulness of statistical methods and analysis in hockey. To them, I simply suggest to look to physics for an example of how people have managed awesome findings amidst chaotic environments. Despite this, we expect some semblance of persistent influence on certain aspects we assume to be driven by talent. When this persistence or repeatability is absent, I believe it’s fair to question a metric’s worth as an evaluative tool.
The Model
Mine is a shot quality model. xG stats are by-products of assigning goal expectancy to shots. In my mind, this ability to assess shot quality is most important, though supplying information with which to devise better evaluative metrics is a welcome benefit. The model is similar in nature to that of @DTMAboutHeart,3I encourage you to read about DTM’s xG model here if you haven’t already. with some important distinctions. The most important difference is his inclusion of regressed shooting talent. I chose to exclude shooter talent not because it isn’t an important factor, but rather because I fear players may unfairly benefit or suffer from their linemates’ aptitude. Here’s what my model does account for:
- Shot type (Wrist shot, slap shot, deflection, etc.)
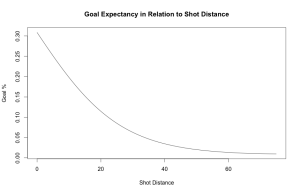
- Shot distance (Adjusted4Distance is not currently adjusted for rink bias. The corrections made here are meant to solve recording errors made by the NHL. All 5v5 shots said to have been taken from a team’s defensive zone were assumed to have occurred in the offensive end in reality. distance from net)
- Shot angle (Angle in absolute degrees from the central line normal to the goal line)
- Rebounds (Boolean – Whether or not the shot was a rebound)
- Rush shots (Boolean – Whether or not the shot was a rush shot)
- Strength state (Boolean – Whether or not the shot was taken on the powerplay)5In hindsight, this is suboptimal. I would likely divide strength states more attentively in any future iterations.
Each of the six shot types6They are: Wrist shot, slap shot, backhand, snap shot, deflection, wrap-around.
provided by the NHL forms its own category, and these are further subsetted by rebound and non-rebound. Only unblocked shots are used due to the unfortunate fact blocked shot coordinates are unavailable.7For clarity’s sake, coordinates for these events exist but represent the location of the blocking player rather than the shooter.
These twelve shot sub-types are regressed independently according to the remaining variables. The rationale here is that each shot subset should respond to the variables differently. Namely, distance and angle do not influence slap shot quality in the same manner as they do, say, deflections. In addition, the relationship between goal expectancy and distance or angle are not assumed to be linear. That is to say, the model is not bound by the idea that shot quality changes at a constant rate along the scales of distance and angle. I found these modifications improved the model’s ability to assess goal expectancy.8Added flexibility in regression models can often have drawbacks, such as overfitting. To avoid this, I tested my model out of sample on a sizeable set of shots not included in the original training data.
EP: Additional details for the mathematically-inclined follow, which you may feel free to scroll past.
Each shot category was binned and ran through a logistic regression using data from the 2007-08 to 2014-15 seasons. Both the distance and angle variables were treated as third-degree polynomials. Each iteration of the model was tested against data from the 2015-16 season using a variety of methods.91. The correlation between mean xFSh% and mean observed FSh% of shot danger bins.
2. The standard error of mean xFSh% and mean observed FSh% of shot danger bins.
3. The average R^2 value obtained from 5 repetitions of testing correlation between mean xFSh% and mean observed FSh% of 1000 samples of 1000 shots.
4. The correlation between xG and observed goals of >400 TOI skaters.
The eventual specifications of the model were selected to optimize the results of these out-of-sample tests.
Shot Quality
The important question at hand is: How well does this model assess shot quality? We may evaluate a number of things to answer this question. Firstly, are “better shots”10In case it was unclear, here I refer to shots deemed by the model to be of higher quality. truly better shots?
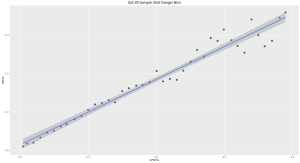
The mean expected Fenwick shooting percentage of shot danger bins does a good job of approximating the observed percentage. It should be reiterated that these are out-of-sample shots. The model has never seen these events because they are excluded from the training data. Additionally, we can see how closely players’ projected goal totals according to the model match actual goals scored:
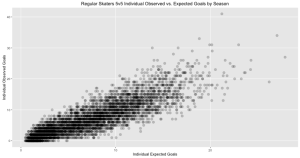
The R^2 value obtained from the above relationship (0.750) significantly exceeds that of goals scored versus unblocked shots (0.586) and even shots on goal (0.619) despite the disadvantage of ignoring whether shots missed the target. Isolating shot quality from quantity by examining the relationship between expected and observed Fenwick shooting percentage in regular skaters yields an R^2 value of 0.130 for forwards and 0.104 for defenders. I believe these are reasonable values considering what factors are not included in the model. Particularly shooter and goaltender talent, as well as pure luck which we know is pervasive in what we’re attempting to measure.
Expected Goals
The logical progression from having developed a method with which to assign goal expectancy to shots is to apply it to the end of player and/or team evaluation. Let xG define Expected Goals, the sum of goal fractions expected from observed unblocked shots. ixG will denote the xG value of unblocked shots taken by a player, while xGF and xGA will represent the xG value of on-ice shots For and Against respectively. xGF% is analogous to GF%, where goals have been substituted with xG. We can easily observe how the inclusion of a shot quality element yields a measure closer to true goal share. 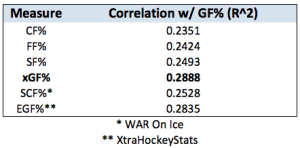 For comparison’s sake, I’ve included Scoring Chance numbers from WAR On Ice and EGF11Abe’s own expected goals model is explained in detail here.
from Nick Abe‘s XtraHockeyStats. While this offers some reassurance that we’re measuring something with our shot quality approximation, it’s really of no use to anybody. After all, we don’t need an indicator of goals when goals themselves are available data. What is of particular interest, to me at least, is whether we can inform better predictions of future goals.
For comparison’s sake, I’ve included Scoring Chance numbers from WAR On Ice and EGF11Abe’s own expected goals model is explained in detail here.
from Nick Abe‘s XtraHockeyStats. While this offers some reassurance that we’re measuring something with our shot quality approximation, it’s really of no use to anybody. After all, we don’t need an indicator of goals when goals themselves are available data. What is of particular interest, to me at least, is whether we can inform better predictions of future goals.
This idea of projecting future outcomes is of great importance in analyses relating to hockey and indeed a great number of fields. In its present condition, 5v5 xGF% is not a better predictor of future 5v5 GF% than CF% at the player level. Regular skaters’ 5v5 xGF% in one >400 TOI season did not yield a higher correlation with the next season’s 5v5 GF% than the same test performed with CF%.12R^2 = 0.103 for CF% compared to 0.081 for xGF%. The same variance observed in early shot quality analyses prevents on-ice xG from predicting real goals, or itself for that matter, in any practical way. Though descriptive of shot quality, the xG model has not yet shown to be appreciably predictive of future shot quality or goals at the on-ice level.13It’s important to note I’m referring to my own xG model. DTMAboutHeart has shown that his own model does have predictive value.
xG does, however, have predictive value at the individual skater level. 5v5 ixG60 is a better predictor of future 5v5 G60 than G60 itself (0.152 for forwards and 0.128 for defence vs. 0.140 and 0.076 respectively).
Why Should I Care?
I believe this is an important question because unless I can provide a satisfactory answer, I’ve wasted your valuable time. I think there’s ample evidence the model does a decent to good job of assessing shot quality given the information available for public consumption. There’s descriptive value here that does not deserve to be ignored, in addition to proven applications at the individual level. Potential uses in team and goaltender evaluation have not yet been discussed. Limitations of the current model have been identified and may point to improvements in successive iterations. One such limitation is the diminished sample resulting from unavailable coordinates for blocked shots. Variance is another issue that can potentially be addressed through regression. It is worth consideration that failure to find reproducibility in on-ice shot quality is not in and of itself a failure. Though disappointing, it is in fact in line with findings such as Tulsky’s discussed above that have long held up to scrutiny. It may serve as consolation, however, to develop practical uses of such a model beyond individual goal scoring.
In the next instalment, I will propose improvements to the model and discuss practical applications of xG in analysis.
References
| 1. | ↑ | Let’s get this out of the way early. “Better” in this article will refer to a greater probability of becoming a goal. |
| 2. | ↑ | People have used this fact to disparage the usefulness of statistical methods and analysis in hockey. To them, I simply suggest to look to physics for an example of how people have managed awesome findings amidst chaotic environments. |
| 3. | ↑ | I encourage you to read about DTM’s xG model here if you haven’t already. |
| 4. | ↑ | Distance is not currently adjusted for rink bias. The corrections made here are meant to solve recording errors made by the NHL. All 5v5 shots said to have been taken from a team’s defensive zone were assumed to have occurred in the offensive end in reality. |
| 5. | ↑ | In hindsight, this is suboptimal. I would likely divide strength states more attentively in any future iterations. |
| 6. | ↑ | They are: Wrist shot, slap shot, backhand, snap shot, deflection, wrap-around. |
| 7. | ↑ | For clarity’s sake, coordinates for these events exist but represent the location of the blocking player rather than the shooter. |
| 8. | ↑ | Added flexibility in regression models can often have drawbacks, such as overfitting. To avoid this, I tested my model out of sample on a sizeable set of shots not included in the original training data. |
| 9. | ↑ | 1. The correlation between mean xFSh% and mean observed FSh% of shot danger bins. 2. The standard error of mean xFSh% and mean observed FSh% of shot danger bins. 3. The average R^2 value obtained from 5 repetitions of testing correlation between mean xFSh% and mean observed FSh% of 1000 samples of 1000 shots. 4. The correlation between xG and observed goals of >400 TOI skaters. |
| 10. | ↑ | In case it was unclear, here I refer to shots deemed by the model to be of higher quality. |
| 11. | ↑ | Abe’s own expected goals model is explained in detail here. |
| 12. | ↑ | R^2 = 0.103 for CF% compared to 0.081 for xGF%. |
| 13. | ↑ | It’s important to note I’m referring to my own xG model. DTMAboutHeart has shown that his own model does have predictive value. |

Very interesting work. When you say that the subtypes of shots are regressed independently on the factors you mentioned, is that equivalent to including interaction variables between each of the factors?
I suspect similar results could be achieved this way, but I haven’t looked into it.
Amazing work. I was just going to suggest interactions and then I saw them here in the comments. Nice. Particularly for shot type, distance and angle (three-way and all two-way interactions). Might improve the correlation.
Also, what software are you using?
I use R.